El análisis de elementos finitos (FEA) es una herramienta poderosa que los ingenieros utilizan para predecir cómo se comportarán las estructuras bajo diversas cargas y condiciones. Pero, ¿qué sucede cuando una estructura no tiene condiciones de borde claramente definidas? Aquí es donde entra en juego el método 3-2-1.
¿Qué es el Método 3-2-1?
Este método se centra en evitar el movimiento de un cuerpo rígido, es decir, grandes desplazamientos o rotaciones sin restricciones, sin limitar la deformación del objeto de estudio. Como resultado, se obtiene una distribución de esfuerzos que no depende de las condiciones de borde aplicadas.
Es útil cuando analizamos sistemas estructurales que no tienen condiciones de borde claras, como por ejemplo una embarcación o una boya flotando en agua, o un avión que se encuentra en pleno vuelo. Estos son casos donde ante la ausencia de soportes, existen grados de libertad que permitirían un movimiento de cuerpo rígido y que no podríamos resolver como un caso estático con elementos finitos.
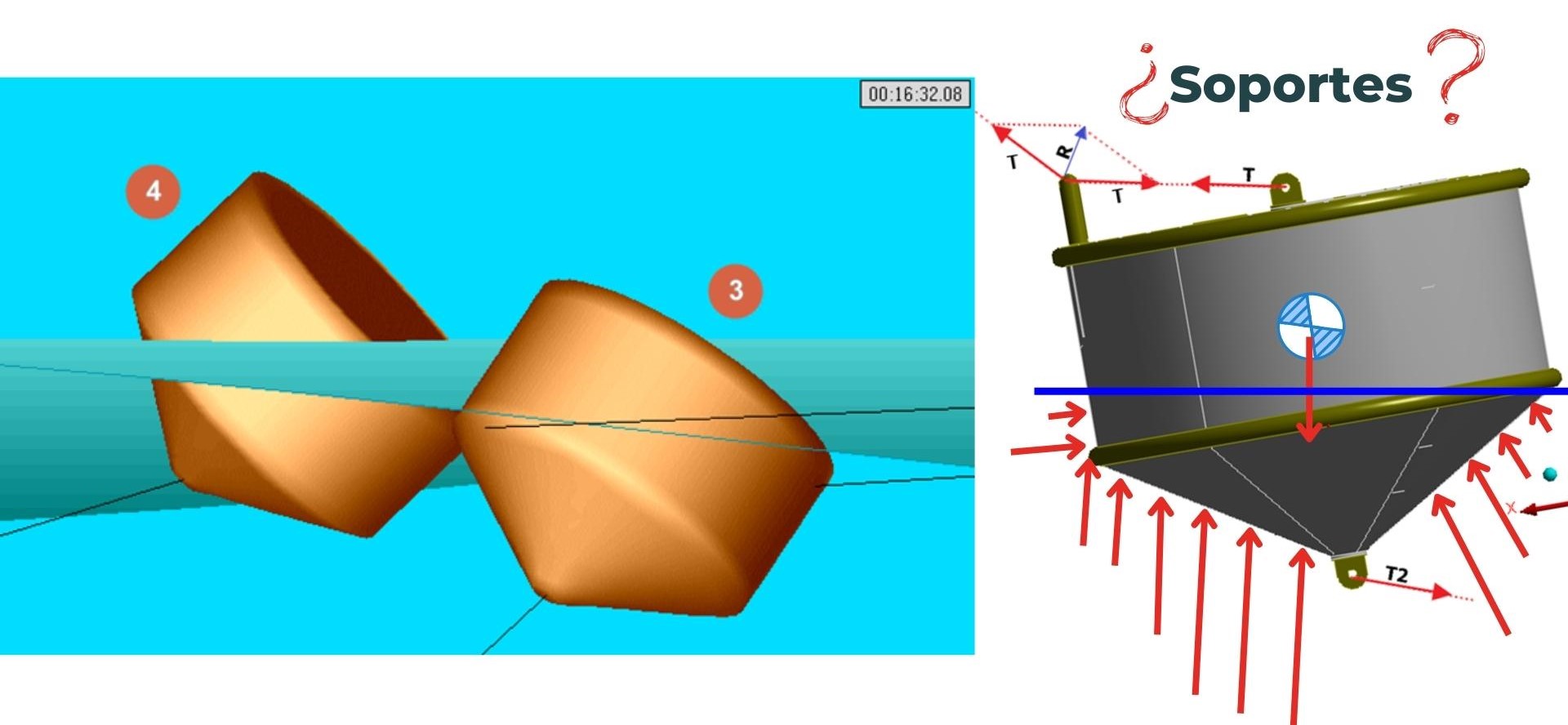
Ejemplo de estructuras flotando en fluidos que no tienen condiciones de borde cinemáticas definidas.
Una característica clave del método 3-2-1 es la necesidad de una carga equilibrada en el objeto, lo que significa que la suma total de las fuerzas y momentos aplicados debe ser cero. Este equilibrio debe ser determinado por el responsable de la simulación, generalmente a través de un diagrama de cuerpo libre, para asegurar que el objeto esté en equilibrio estático. Con una carga equilibrada, las fuerzas de reacción en las condiciones de contorno fijas, o soportes, serán nulas o muy cercanas a cero.
La implementación del método 3-2-1 depende de la correcta ubicación de tres soportes esenciales.
El primer soporte ancla un nodo de la malla en el espacio, limitándolo en las direcciones X, Y, Z, es decir, tres grados de libertad globales.
El segundo soporte se sitúa en un eje local que parte del primer punto, y restringe el nodo en las direcciones perpendiculares, o sea, las direcciones Y y Z, suponiendo que el nodo se sitúa en el eje X.
El tercer soporte se coloca en un plano que atraviesa los dos primeros puntos y previene la rotación, es decir, si el nodo se sitúa en el plano XZ, estará limitado en la dirección Y. Para confirmar que el modelo está configurado de manera adecuada, se puede realizar (o visualizar) un análisis térmico para asegurar que permitirá la expansión térmica libre sin generar fuerzas en los soportes.
¿Por qué es útil el Método 3-2-1?
El método 3-2-1 es una técnica útil en el análisis de elementos finitos (FEA) que ayuda a aplicar restricciones a un modelo de manera que podemos simular estructuras hipostáticas o que presentan cierto movimiento (grado de libertad) no restringido. De esta manera podemos evitar incluir condiciones de borde "fáciles" como un anclaje o restringir grados de libertad cuando realmente no es así.
Aquí te presento algunas razones por las que podríamos necesitar el método 3-2-1:
- Evitar la rigidez artificial: En FEA, a menudo es necesario restringir un modelo para evitar el movimiento de un cuerpo rígido. Sin embargo, las restricciones convencionales pueden introducir rigidez artificial en el modelo, lo que puede distorsionar los resultados de las tensiones. El método 3-2-1 ayuda a evitar esta rigidez artificial al aplicar las restricciones mínimas necesarias.
- Obtener tensiones más precisas: El método 3-2-1 puede ayudar a obtener una distribución de tensiones más precisa y realista en el modelo. Esto es especialmente útil en situaciones donde las restricciones convencionales pueden distorsionar los resultados de las tensiones.
- Autoverificación: El método 3-2-1 es autoverificador. Si se producen grandes fuerzas de reacción en los nodos seleccionados por el étodo, esto indica que las fuerzas externas aplicadas no están en equilibrio y deben corregirse. Esto puede ayudar a identificar y corregir errores en la aplicación (estimación) de las cargas.
El método de 3-2-1 te puede ayudar a resolver casos con submodelos, o con componentes parciales de una estructura. Aunque formalmente a técnica de submodelado es más completa que el método de 3-2-1, el método 3-2-1 te puede servir en casos simples sin la necesidad de generar un modelo global. Puedes revisar este artículo donde te explico el detalle del submodelado.
Aplicando el Método 3-2-1: Un Ejemplo Práctico con una Oreja de Izaje
Para entender mejor cómo funciona el método 3-2-1, revisemos un ejemplo práctico:
Imagina que tienes una oreja de izaje, instalada en un portico que se va a someter a una carga de tracción. Quieres usar FEA para predecir cómo se comportará la oreja de izaje bajo esta carga, pero no quieres simular todo el modelo (columnas, ni viga completa), ni colocar soportes que distorsionen tus resultados en las fronteras del sector que has escogido. Aquí es donde el método 3-2-1 puede ser útil.
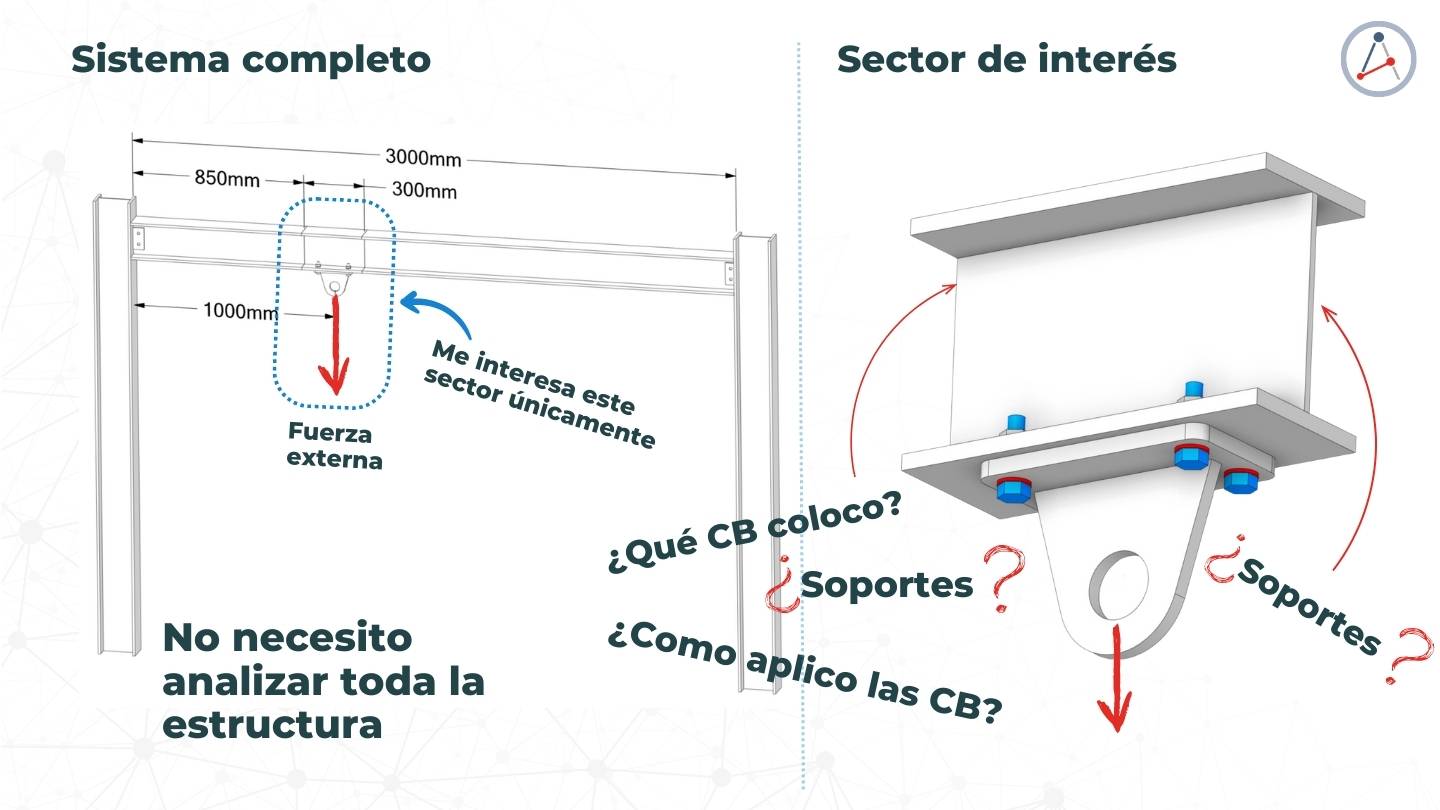
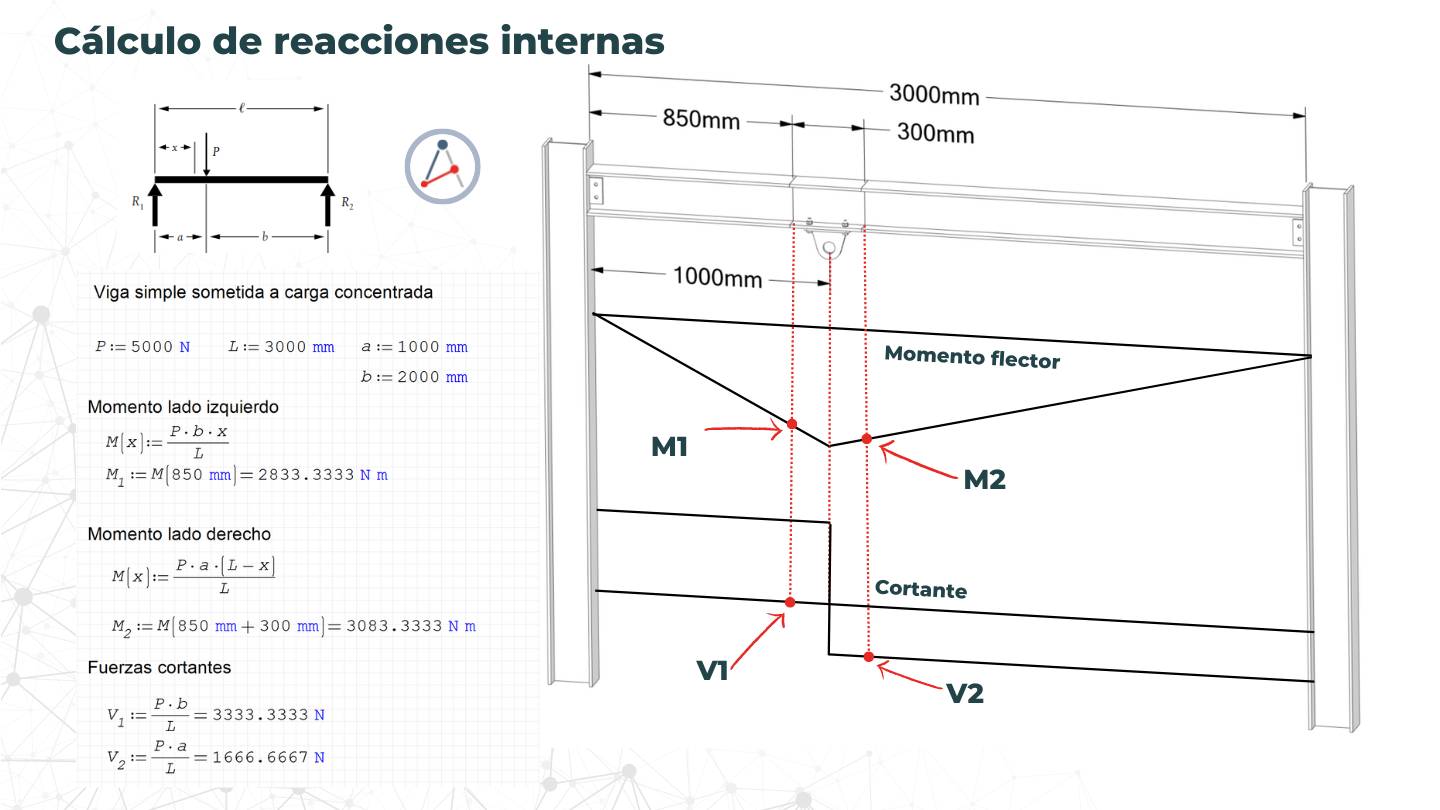
PASO 1: Calcula las cargas que equilibran el sistema.
Antes de aplicar cualquier carga a tu modelo, necesitas calcular las fuerzas que equilibrarán el sistema. Esto es crucial para poder aplicar una carga equilibrada en el paso siguiente. Si no tienes un conocimiento preciso de estas fuerzas, no podrás aplicar correctamente el método 3-2-1.
PASO 2: Aplica las cargas equilibradas:
Después de calcular las fuerzas que equilibrarán el sistema, puedes aplicar las cargas. Estas cargas deben estar equilibradas para evitar la creación de una fuerza de reacción neta excesiva en las restricciones que colocarás en los nodos 1-2-3 que identificaremos en el siguiente paso. En este paso debes escoger la mejor estrategia para aplicar las cargas: distribuida en nodos: uniforme o variable, con condiciones rígidas (RB3), etc. Esto afectará localmente los esfuerzos en las fronteras.

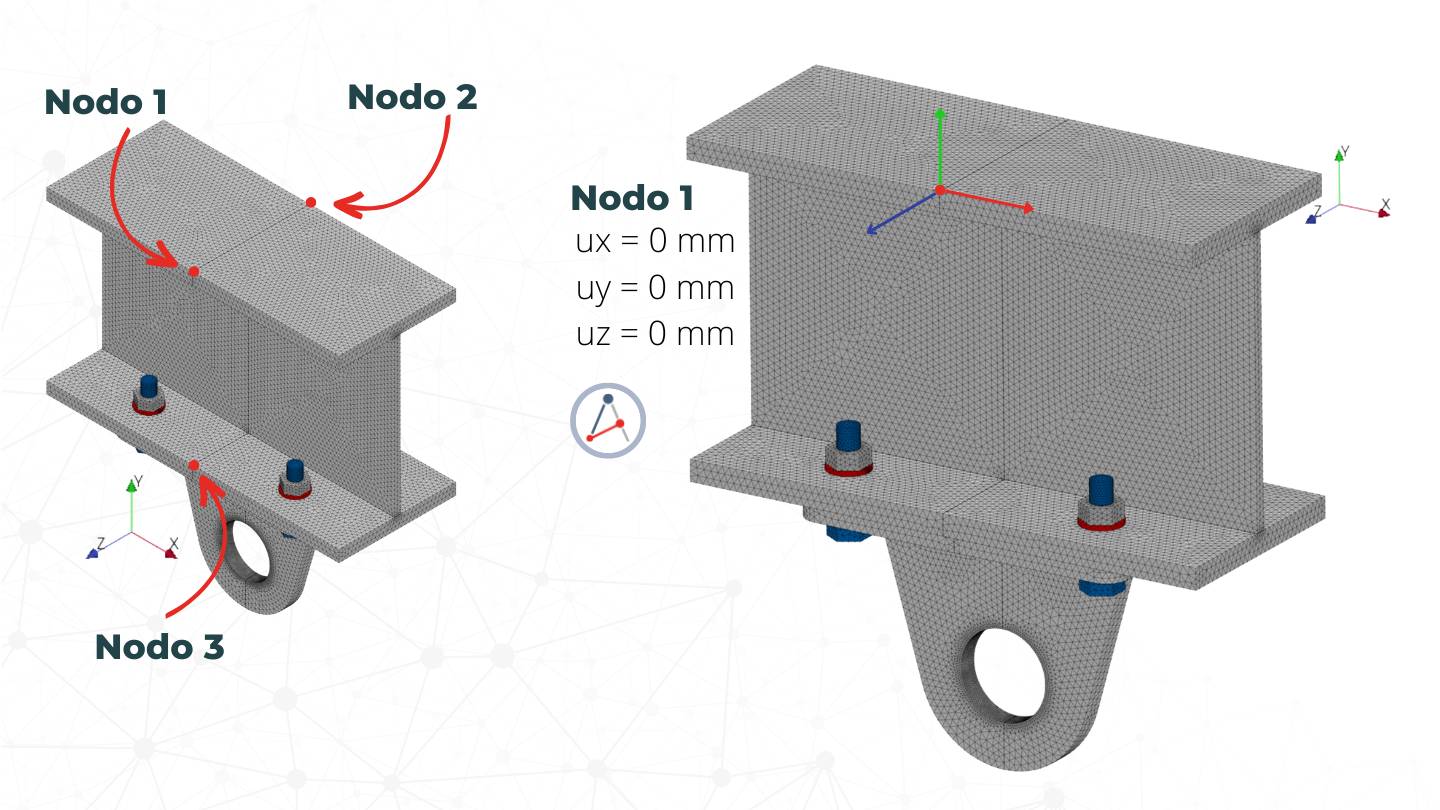
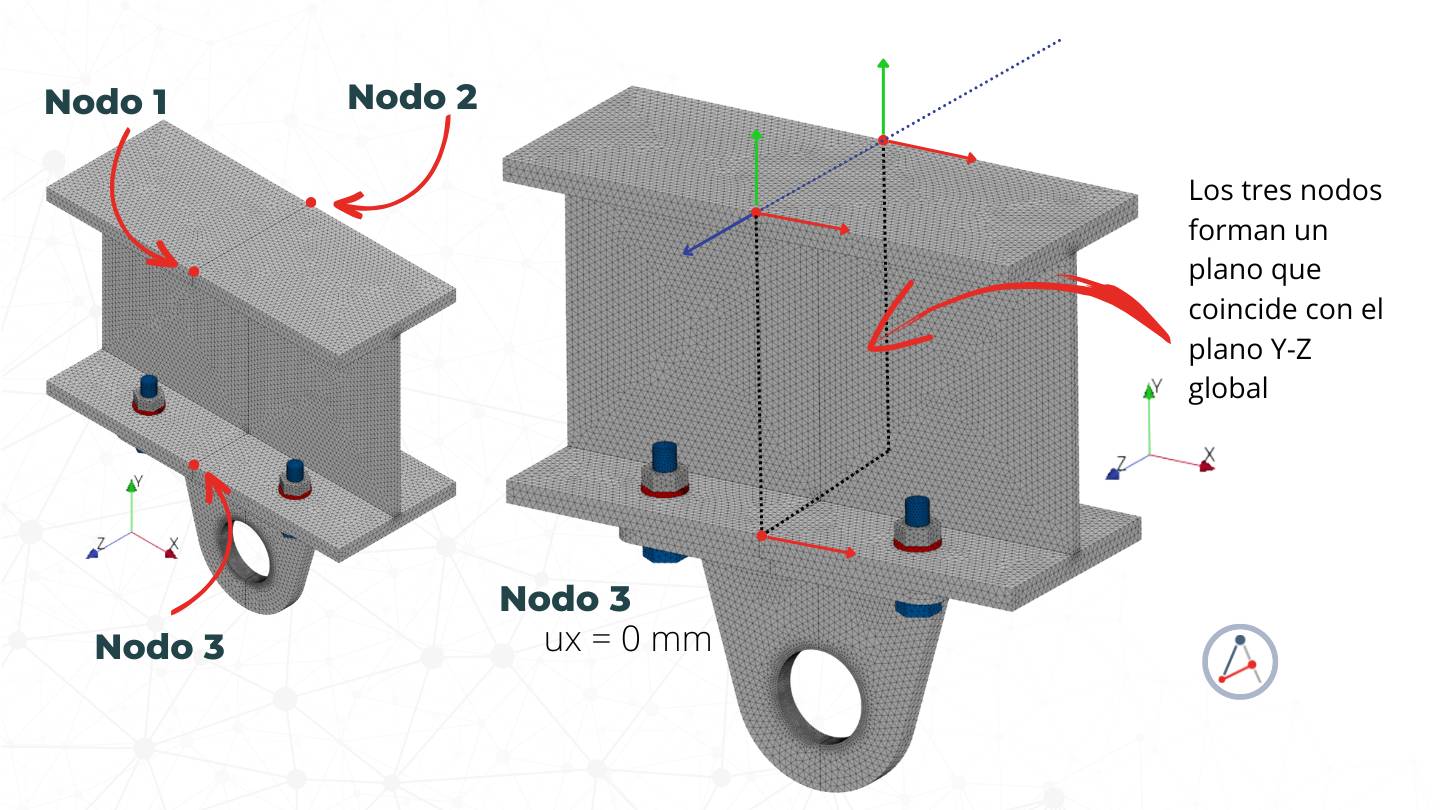
PASO 3: Identifica tres nodos en tu modelo:
En este caso, podrías elegir tres puntos en la viga que estén bien espaciados y orientados cuidadosamente. Estos nodos no deben ser colineales, es decir no deben formar una línea recta. Por ejemplo, siempre busco seleccionar los nodos que queden automáticamente alineados con los ejes de coordenadas globales y formen parte de un plano conocido, solo para facilitarme el análisis de los grados de libertad que se restringirán en cada uno.
En la figura a continuación te muestro los nodos que he seleccionado en la sección de la viga, pero pudiesen ser otros (hay infinitas alternativas) y esto no va a afectar los resultados (puedes probar varias opciones) siempre y cuando las cargas que obtuviste previamente estén bien calculadas y estén equilibradas.

PASO 4: Restringe los grados de libertad del primer nodo:
Al primer nodo, restringe los tres grados de libertad (GDL) traslacionales. Esto significa que este punto no puede moverse en ninguna dirección. Este nodo será la referencia de desplazamiento de tus resultados, a pesar de que el método 3-2-1 está pensado para los esfuerzos y no para analizar los desplazamientos.
Esta restricción automáticamente evitará que el modelo se desplace como cuerpo rígido en las tres direcciones, pero el modelo aún es libre de rotar como rígido, esto lo corregiremos aplicando CB a los dos restantes nodos seleccionados.
PASO 5: Restringe los grados de libertad del segundo nodo:
El segundo nodo tiene dos GDL translacionales restringidos, en las dos direcciones que son normales a la línea que conecta el nodo 1 al nodo 2. En nuestro ejemplo, la línea imaginaria que pasa por nuestros nodos 1 y 2 coincide con el eje Z global, por lo que solo debes restringir los desplazamientos en dirección X, Y para este nodo. Esto significa que este punto puede moverse únicamente a lo largo de la línea que conecta el nodo 1 al nodo 2, pero no puede moverse en ninguna otra dirección.
Esta inclusión evita la rotación de cuerpo rígido respecto al nodo 1 en el eje Y y rotación en el eje X.

PASO 6: Restringe los grados de libertad del tercer nodo:
El tercer nodo tiene un solo GDL restringido, y es normal al plano que forman los nodos 1, 2 y 3. En nuestro ejemplo, esto coincide con el plano Y-Z global, por lo que debe restringirse únicamente la dirección normal a este plano imaginario, es decir los desplazamientos en X son nulos para este nodo. Esto significa que este punto puede moverse en cualquier dirección dentro del plano definido por los nodos 1, 2 y 3, pero no puede moverse fuera de este plano.
Con esta restricción evitamos la rotación como cuerpo rígido respecto al eje Z.
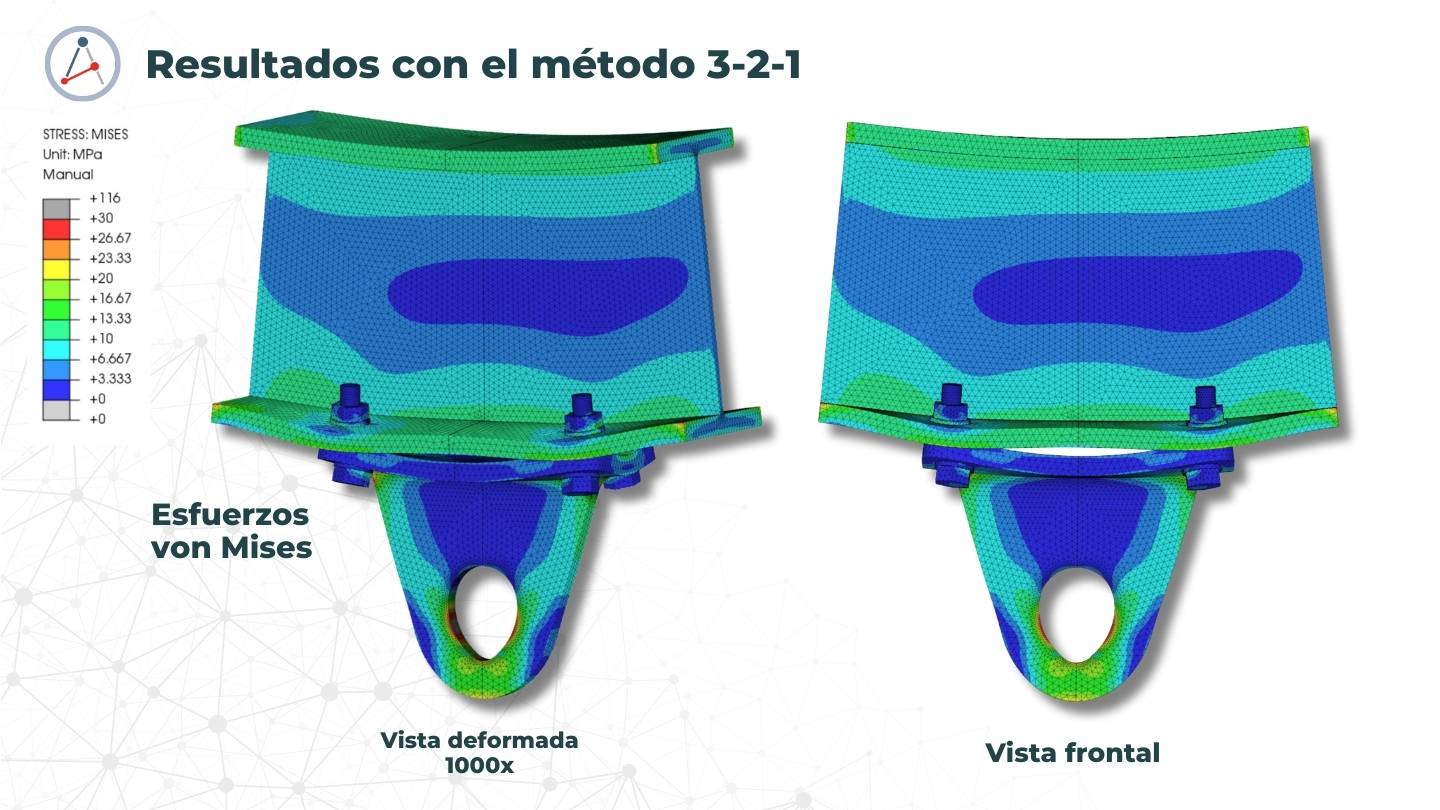
PASO 7: Realiza el análisis FEA:
Una vez que hayas aplicado las restricciones y la carga equilibrada, puedes proceder con el análisis FEA. El método del 3-2-1 se centra en la visualización de esfuerzos en los componentes, no es recomendado para revisar desplazamientos, pues estos son relativos a los GDL restringidos en los nodos seleccionados, por lo que el campo de desplazamientos siempre será relativo a estos nodos.
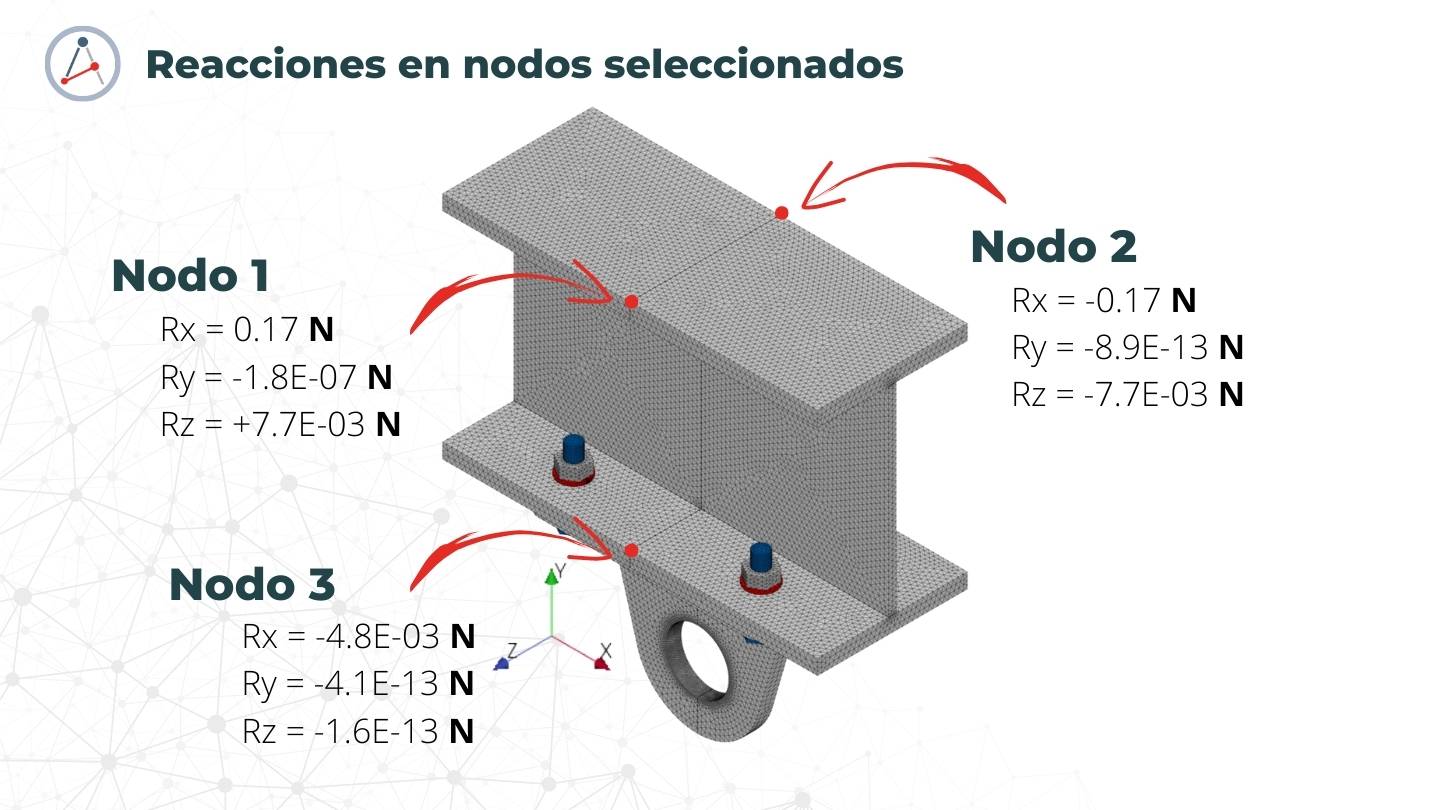
Como práctica recomendada, se deben revisar las reacciones en los 3 nodos seleccionados. Su magnitud debe ser muy pequeña respecto a las cargas externas y reacciones de equilibrio aplicadas. En este ejemplo, los nodos 1 y 2 presentan un desbalance en dirección X de 0.17 N, con signos opuestos respectivamente, indicando que absorben algún desbalance numérico ya que se han truncado las cargas cortantes y momentos aplicados en las fronteras. Adicionalmente, no observamos ninguna concentración de esfuerzos en estos nodos, descartando singularidades y confirmando que la estimación de cargas es adecuada para garantizar el equilibrio.
Este es un ejemplo simplificado, pero debería darte una buena idea de cómo se aplica el método 3-2-1 en la práctica. Recuerda que la precisión en la selección y restricción de los nodos, así como en la aplicación de la carga, es crucial para el éxito de este método.
¿Que pasa si quiero simular todo el modelo?
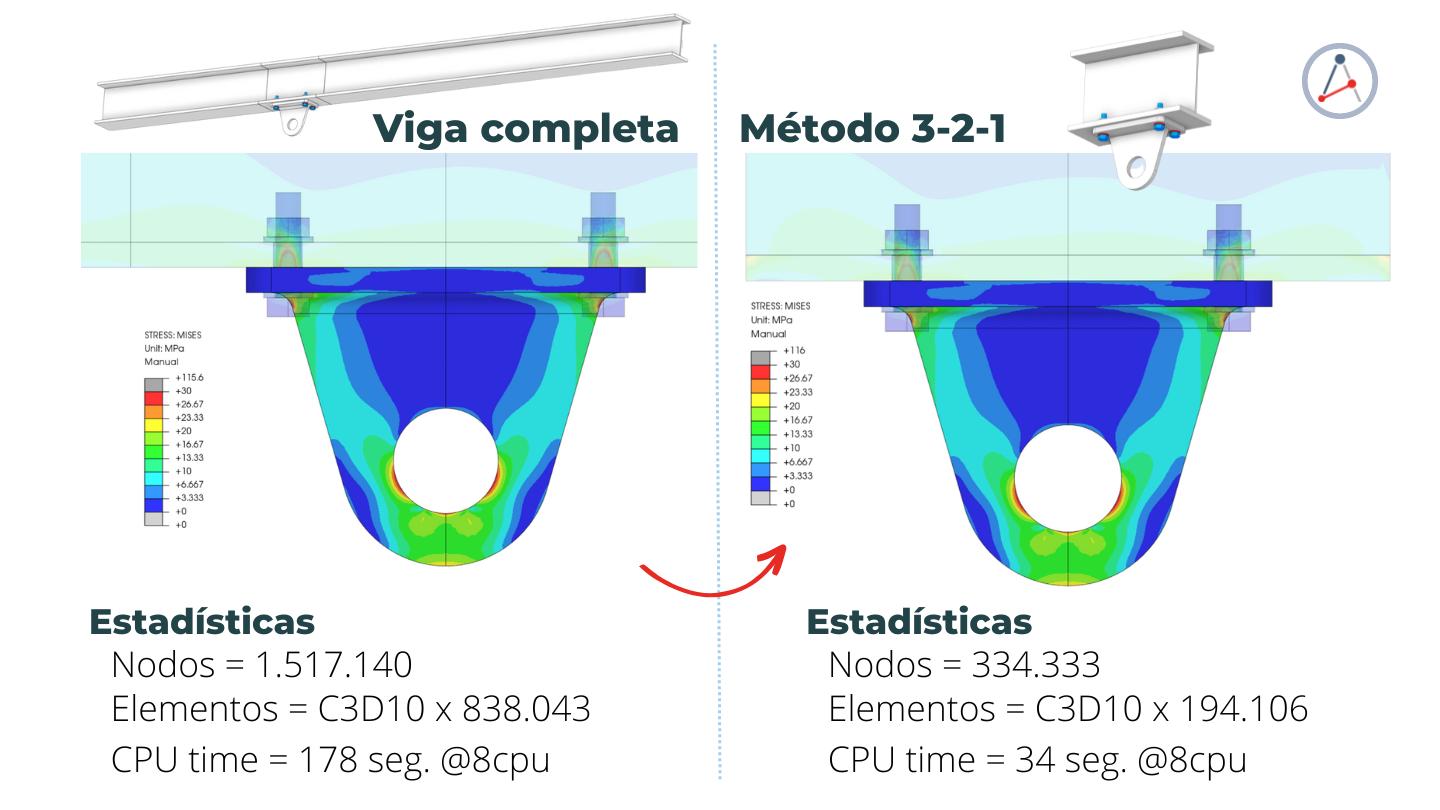
En realidad no pasa nada. Depende de ti y de lo que necesites. En este ejemplo que te he presentado, está la opción de simular todo el pórtico o solo la viga con la oreja instalada. Hay otras situaciones en las que realmente no será posible. Si incluyes un modelo con la viga completa, simplemente apoyado en sus extremos con una condición RB3 y manteniendo libre solo las rotaciones en el sentido de la flexión principal, obtendrás resultados muy, pero muy, similares. Te muestro abajo las diferencias.
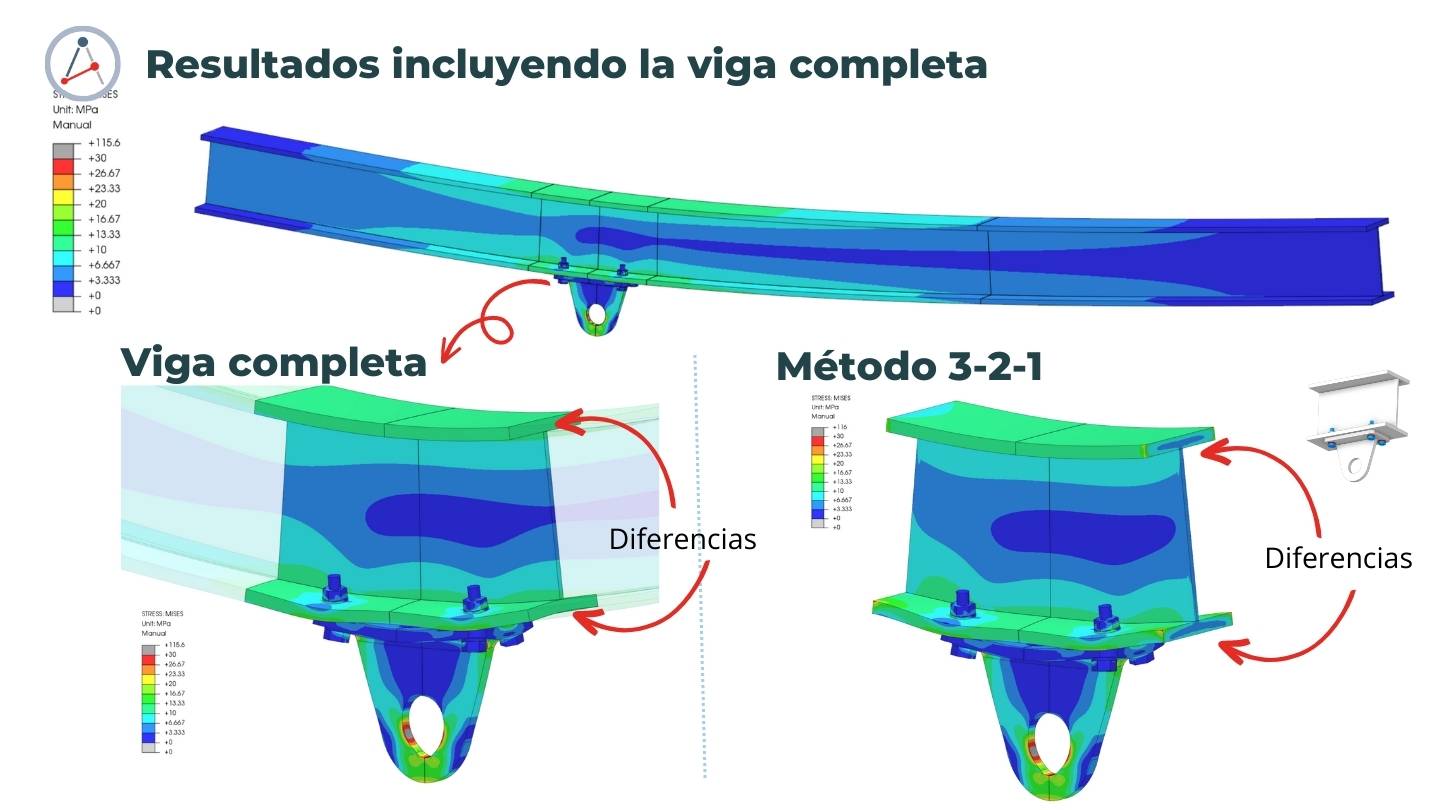
Vas a notar que los resultados son muy similares. Solo se observan diferencias en las fronteras del modelo con el método 3-2-1, como consecuencia directa de la rigidez local y estrategia de aplicación de las cargas en esa zona. Si cambiamos la forma en como aplicamos las cargas o extendemos las fronteras, las diferencias se irán diluyendo. Esto representa el principio de Saint-Venant en acción. Puedes revisar este otro artículo donde te explico en detalle este principio.
Si analizas solo las orejas, bien alejadas de las zonas de carga, pues no notarás diferencias. Validando que el método 3-2-1 es realmente util en situaciones similares cuando queremos trabajar sectores independientes pero no sabemos que condiciones de borde aplicar o que estas son muy complejas de aplicar directamente. El método 3-2-1 te puede servir para representar submodelos, pero con limitaciones, pues solo podrás revisar esfuerzos con el. Esto te permitiría trabajar con modelos pequeños, en especial si tienes limitaciones de hardware o tiempo.
Ventajas del Método 3-2-1
Una de las principales ventajas del método 3-2-1 es que puede proporcionar resultados de tensiones más confiables en un modelo FEA. Al permitir que el modelo se deforme de manera más natural bajo las cargas aplicadas, este método puede ayudar a obtener una distribución de esfuerzos más realista, más aún cuando la estructura o modelo no tiene condiciones de borde cinemáticas evidentes o sencillas de aplicar. Con esto no tienes que aplicar "empotramientos" o "anclajes" cuando no sabes que aplicar (lo cuál es una salida rápida pero inadecuada muchas veces).
Además, el método 3-2-1 es bastante flexible y puede ser aplicado a una amplia gama de modelos y situaciones. Siempre que se puedan identificar tres nodos adecuados y se pueda aplicar una carga equilibrada, este método puede ser una opción viable.
Puedes usar el método como herramienta para analizar una parte de una estructura (como en el ejemplo que te he desarrollado) a modo de submodelo, sin tener que resolver toda la estructura completa.
Desventajas del Método 3-2-1
A pesar de sus ventajas, el método 3-2-1 no está exento de desafíos. Uno de los más significativos es la necesidad de tener un conocimiento preciso de las fuerzas que equilibrarán el sistema antes de poder aplicar una carga equilibrada. Esto puede ser un desafío, especialmente en situaciones donde las cargas son complejas o difíciles de calcular. Además, cualquier error en la selección y restricción de los nodos, o en la aplicación de la carga, puede resultar en una fuerza de reacción neta en las restricciones, lo que puede causar enormes tensiones locales y arruinar los resultados del modelo.

Hola Asdrubal, muy buen artículo. Me parece interesante conocer técnicas y «trucos» de este tipo. He trabajado con simulaciones de mecanismos y muchas veces es complejo analizar una sola pieza, aún si conocemos que no tiene un soporte o condiciones «fáciles» de asignar, pero si conocemos las cargas que le transmiten los otros componentes y este se encuentra de igual manera en equilibrio. Este método parece que nos podría funcionar en esta situación. Una vez más, gracias por tu aporte a la comunidad de simulaciones y no te detengas. Nos vemos en la academia CAE. Saludos!
Hola Sebastián, gracias por tu comentario, en efecto el método en casos como el que mencionas nos puedes ayudar, a veces lo utilizo cuando no quiero hacer submodelos y estoy corto de tiempo y el cálculo de las cargas que equilibran el sistema es facil de obtener. De igual manera, puedes probarlo con algún caso conocido y si te parece, plantearlo en la comunidad de la academia CAE. Saludos!
A propósito que estaba conversando con unos colegas ingenieros navales sobre cómo se deben colocar las Boundary Conditions en piezas como barcos, en dónde no hay un soporte como tal, sino que el peso propio de la embarcación es equilibrada (o contrarrestada) por la presión hidrostática que ejerce el agua sobre el área mojada (obra viva).
El método 3-2-1 se podría aplicar para hacer el análisis estructural del casco de un barco? La dificultad de calcular las fuerzas que equilibran el sistema se hace muy marcada ya que la presión hidrostática varía no sólo con respecto a la profundidad, si no que varía de dirección al cambiar la forma del casco. He investigado el tema y en varias tesis usan «Inertia Relief» para equilibrar las cargas del sistema. ¿Qué método sería el más adecuado?
De antemano, muchas gracias. El contenido que haces es de muy buena calidad.
Hola José, muchas gracias por dejarme tu comentario.
Si se puede aplicar el método 3-2-1 en el caso de un barco (o componentes flotando). Como mencionas, es un tema que se enfoca en «qué tan difícil sea para nosotros obtener ese estado de equilibrio de nuestro sistema». El método de inertia relief es muy parecido, pero lo que haces es calcular aceleraciones ficticias que generan fuerzas inerciales (m*a) que contrarrestan algún posible desbalance de fuerzas en el modelo, de igual manera tienes que colocar algún soporte en el barco para prevenir movimiento de cuerpo rígido, siendo los desplazamientos obtendios relativos a este soporte, dependiendo tambien de donde lo coloques. Ambos métodos son recomendados para analizar esfuerzos y no tanto para desplazamientos, pues siempre dependerá de lo que coloquemos como «soportes».
Recomendarte cuál incluir, depende de cada caso. El método del 3-2-1 no depende de la herramienta, no necesitas nada especial y lo puedes aplicar hasta en solidworks (para el artículo lo hice con PrePomax & Calculix). El inertia relief es una opción que puedes activar en muchos programas, pero algunos no la tienen, o si la tienen es limitada por el tipo de análisis en la que se puede incluir. Pero esto sería limitación de software y no del método como tal.
Si quieres practicar, toma un caso relativamente simple y resuélvelo por ambos métodos, describe sus ventajas y desventajas.
Saludos,